Escarbando en la complejidad
Por Andrés Schuschny
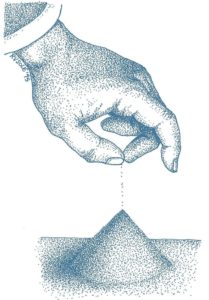
Supongamos que tenemos un balde lleno de arena seca y lo damos vuelta de manera súbita en una mesa. Nada extraño parece ocurrir; simplemente vemos como resultado que se formó una pila de arena. Consideremos ahora que, muy sutil y suavemente, vamos lanzando desde arriba de a un granito de arena por vez. ¿Qué ocurriría? Eventualmente, se sucederán pequeñas avalanchas o deslizamientos de arena. La adición sucesiva de granitos de arena provoca un aumento de la tensión que termina causando avalanchas que se propagan a lo largo y ancho de la pila y cuyo tamaño puede variar de lo ínfimo hasta abarcar grandes superficies. La pila alcanza un estado estacionario, donde la cantidad de arena añadida está balanceada por la cantidad de granos de arena que se salen de la pila. En este “estado estacionario”, existen avalanchas de todos los tamaños. Si registráramos el historial del tamaño de las diferentes avalanchas que se producen cuando vamos añadiendo granitos de arena a la pila, ciertamente veríamos que, dadas las características de este sistema complejo, no existirá un tamaño típico o medio en las avalanchas.
Ciertamente, la mayoría de las avalanchas serán de pequeña magnitud, pero veremos también que se suceden (algo más esporádicamente) avalanchas de tamaños intermedios y, de vez en cuando, avalanchas cuya magnitud son comparables al tamaño de toda la pila de arena. La distribución del tamaño de las avalanchas no tiene ninguna semejanza con la famosa campana de Gauss, aquella que nos permitía definir el valor promedio y el tamaño del fenómeno parametrizado por la varianza de la distribución. En efecto, sistemas como la pila de arena poseen una varianza que teóricamente resulta infinita.
Así como la pila de arena, existen numerosos fenómenos que no poseen un tamaño característico a partir del cual se nos facilite su parametrización y, por lo tanto, se posibilite su control tal como si se tratara de un mecanismo maquínico. La universalidad de ciertos comportamientos se reafirma en diversos y distintos sistemas de muy variada naturaleza donde la contingencia, la rareza, la multiplicidad de eventos y los saltos de escala son la pauta de organización de estos sistemas. Además, es posible representar o simular computacionalmente este tipo de sistemas, lo cual resulta muy útil y didáctico para avanzar en dirección a la comprensión de los principios de organización de la complejidad subyacente.
Sea que se trate de la volatilidad de los mercados financieros, las intensidades de los conflictos y las guerras, las visitas a las páginas web, las citaciones en publicaciones científicas, el tamaño de las empresas, la distribución de la riqueza, el tamaño poblacional de las ciudades y pueblos y la magnitud de las convocatorias a las más diversas movilizaciones ciudadanas; todos estos ejemplos comparten mucho de lo que se describe con la simple analogía de la pila de arena. Cada uno de estos sistemas es un todo consistente de un inmenso número de componentes en mutua interacción. Se trata de sistemas complejos que se autoorganizan en lo que se denomina como un “estado crítico”, altamente interactivo y relacional donde una perturbación menor puede conducir al acontecimiento de eventos, o avalanchas, de todos los tamaños posibles.
En física de los sistemas complejos el fenómeno lleva el nombre de: Criticalidad Autoorganizada. Se trata de una de las explicaciones más elegantes que hay acerca del porqué la evolución de muchos sistemas complejos da lugar a distribuciones denominadas “power law” o leyes de potencias cuyas colas son anchas, es decir cuyos valores extremos son mucho más probables que bajo condiciones gaussianas, dado que son distribuciones estadísticas que teóricamente poseen una varianza infinita, lo que hace que los fenómenos que se basan en estas distribuciones no poseen un tamaño típico o característico. Con todo esto me estoy refiriendo a los famosos Cisnes Negros bautizados por Nassim Nicholas Taleb. Por otro lado, existen otro tipo de representaciones surgidas de la física de los sistemas complejos y la teoría de redes que exhiben comportamientos parecidos y que también nos sirven como metáforas explicativas de muchos otros fenómenos de la realidad.
Vale pues indagar y conocer este tipo de modelos de sistemas complejos y detenerse a reflexionar sobre sus posibles implicancias. Ciertamente, la utilización de la pila de arena no es más que una metáfora explicativa, un modelo de juguete que, como otros modelos similares, puede abarcar una gran variedad de fenómenos atribuibles a otros numerosos contextos de la realidad actual. Está claro que ya no nos resulta sorprendente afirmar que vivimos un período histórico trascendente signado por colosales cambios, disrupciones y rupturas, discontinuidades y crisis. Observamos que, si bien los sistemas sociales, políticos y económicos evolucionan de modo incremental, hoy somos plenamente conscientes de que la tecnología revoluciona de manera disruptiva y exponencial. Vale destacar que lo determinante de una innovación hoy, no es ya la creatividad que deriva en una tecnología, sino la capacidad de sus creadores de convencer a la sociedad de la necesidad de su uso y, al adoptarlos por una creciente mayoría, de persuadir al resto de la necesidad de transformar aquello que esa tecnología provoca transfigurar.
El gran dilema se presenta cuando nos damos cuenta de que hemos desarrollado visiones del mundo o modelos mentales que ya no responden al imperativo de esta transformación emergente que testimoniamos. Una provocativa y ya muy conocida maldición china reza: “¡Que vivas en una época muy interesante!” Nosotros, que estamos surfeando en una de ellas, estamos en condiciones de comprender la ironía de esas sabias palabras. El espacio conceptual desde el que todos venimos y que nos formó (y tal vez un poco deformó), se correspondía con una lógica aditiva, lineal y geométricamente euclidiana, que se soñaba como única y soberana. Las coordenadas cartesianas de esa realidad nos ofrecían una trama conceptual tranquilizadora, y la ciencia, en tanto dogma dominante, nos presentaba un universo mecánico, manipulable y predecible, aunque se antojaba un mundo domesticado y, hasta cierto punto, desencantado.
Avanzar en una comprensión más profunda de los principios de organización que subyacen en la complejidad resulta no sólo un ejercicio esclarecedor sino también debería comportar un cambio de perspectiva en el que ya no podemos apelar a la dicotomización entre lo “normal” y lo “patológico”, ni se puede pensar al mundo como conformado por entes separados, dispuestos en espacios analíticamente independientes y estancos. Por suerte, contamos con toy models que, usándolos como representaciones metafóricas, nos facilitan simular e internalizar este tipo de modos de comprensión.
Andrés Schuschny